Les méthodes de réglage d’un correcteur PID que l’on décrit dans la littérature sont souvent difficiles à appliquer ou prennent trop de temps.
Je propose ici une méthode adaptée de la méthode de « juste oscillation » qui présente les avantages suivants:
- Les essais se font uniquement en boucle fermée, donc pour un four c’est beaucoup plus rapide, et c’est applicable pour les systèmes où ouvrir la boucle n’est pas possible.
- On ne provoque pas de franche instabilité comme dans la méthode de « juste oscillation » donc pas de risque de détériorer le système
- On ne fait que des réponses à un échelon de tension, ce qui est simple à mettre en œuvre.
Dans ce qui suit, Ti est la valeur de l’action intégrale et Td l’action dérivée, toutes deux en secondes.
 Une valeur trop faible de Ti déstabilise le système.
Une valeur trop faible de Ti déstabilise le système.
Méthode pour les systèmes qui peuvent dépasser
On commence par supprimer les actions intégrale et dérivée. On met une action proportionnelle faible pour s’assurer de mettre le système en route dans une configuration stable.
1 – On enregistre une réponse à un échelon de consigne. S’il n’y a pas de dépassement, on augmente l’action proportionnelle jusqu’à obtenir une réponse ressemblant à ceci:
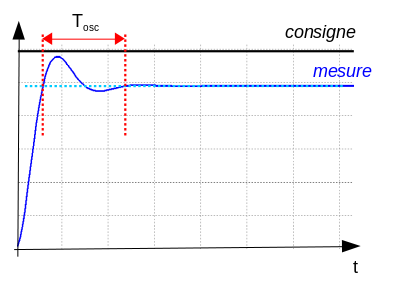
2 – On mesure la pseudo-période de cette oscillation Tosc entre 2 passages par la valeur finale ou entre 2 crêtes, et on règle :
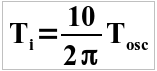
3 – On refait un essai de réponse et l’erreur doit avoir disparu, sans dégradation de la stabilité :
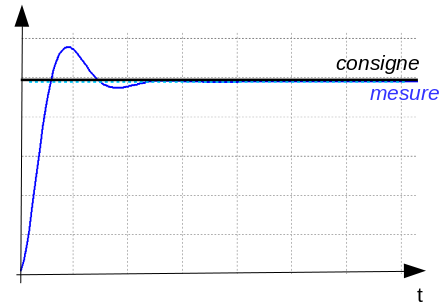
4 – Si le dépassement a augmenté notablement, c’est que Ti est trop petit.
5 – Pour finir, si l’on veut atténuer les oscillations, on peut baisser un peu l’action P, ou ajouter une action dérivée, réglée à Td =Ti /10. Si Td n’est pas assez efficace, augmenter Td.
Méthode pour les systèmes qui ne peuvent pas dépasser
Le principe ici est d’assimiler le système à un premier ordre.
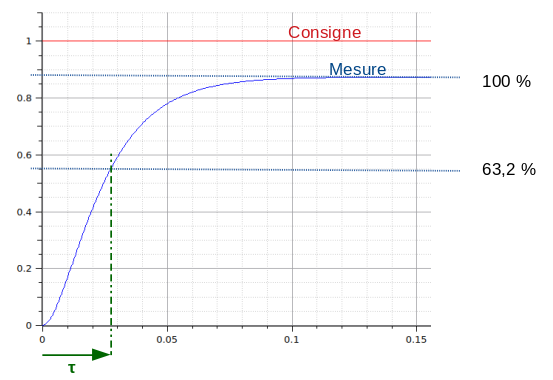
On mesure la constante de temps en boucle fermée τ ; c’est le temps pour arriver à 63% de la valeur finale.
Et on règle Ti = 3 τ
La théorie prévoit que le système sera un peu déstabilisé par ce réglage. Si le dépassement est <5 %, c’est parfait. Sinon, augmenter Ti.
Eléments de démonstration
Tout est basé sur le critère de stabilité de Bode (marge de phase). La fonction de transfert en boucle ouverte est notée T et la pulsation de transition est notée ωT. ( ωT est la pulsation pour laquelle 20log|T(ωT)| = 0dB )
Pour la première méthode, il s’agit de modéliser le système par un passe-bas du second ordre.
- On calcule la pulsation ωosc des oscillations amorties dans la réponse indicielle.
- On calcule ωT.
- Si l’amplification statique de la fonction de transfert en boucle ouverte T est >>1 , c’est à dire |T(0)|>>1, alors on démontre que ωosc est en première approximation assimilable à la pulsation de transition ωT.
- A une pulsation de ωT/10, le correcteur PI n’apporte qu’un retard de phase de quelques degrés, donc en respectant 1/Ti = ωT/10 on est assuré de ne dégrader que très peu la stabilité.
Pour la deuxième méthode, on assimile le système à un premier ordre et on peut démontrer alors que ωT ≈ 1/τ. En prenant 1/Ti = ωT/3 on déstabilise volontairement le système pour optimiser le temps de réponse.